Quantum Entanglement is a phenomena in which the states of 2 particles is such that one of them cannot be described without the other. Multiple Qubits can be entangled as well. In this chapter of the Qiskit Tutorial, you will learn how you can initialize the state of multiple Qubits that are entangled.
Initialize Qubits in Entangled State
Qubits can be initialized in an entangled state by using the initialize() method of the QuantumCircuit class. The initialize() method is passed the state vector for the entangled Qubits along with the Qubits that need to be entangled. In the following examples, we will create a Quantum Circuit with 2 and 3 Qubits and initialize them to Bell state and Greenberger–Horne–Zeilinger (GHZ) state respectively, both of which are maximally entangled states.
Initializing to Bell State
Bell State is a set of 4 possible maximally entangled states that a 2 Qubit system can be present in. In this example, we will specifically deal with ɸ = (|00> + |11>)/√2 state. This Bell State can be achieved by the following Quantum Circuit-
# Creating Quantum Circuit
qc = QuantumCircuit(2, 2)
# Creating a Bell State
qc.h(0)
qc.cx(0, 1)
qc.draw(output = 'mpl')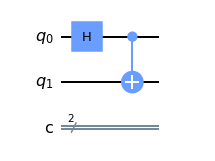
We can also create the same quantum state by calling the initialize() method on the Quantum Circuit and passing it the state vector for the state and the Qubits which have to be entangled.
# Creating Quantum Circuit
qc = QuantumCircuit(2, 2)
# Creating a Bell State
qc.initialize([1/np.sqrt(2), 0, 0, 1/np.sqrt(2)], qubits=[0, 1])
qc.draw(output='mpl')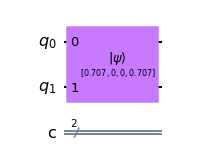
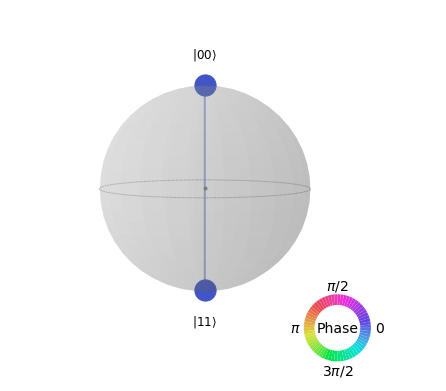
The Q-Sphere corresponding to the given state of Qubits is shown below, and confirms that the desired Bell state has been achieved-
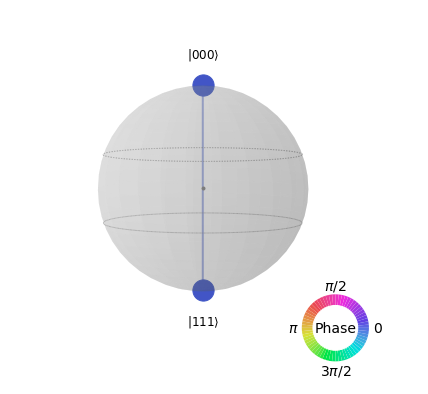
Initializing to GHZ State
The GHZ state is a maximally entangled state of 3 Qubits defined by ɸ = (|000> + |111>)/√2 state. This GHZ State can be achieved by the following Quantum Circuit-
# Creating Quantum Circuit
qc = QuantumCircuit(3, 3)
# Creating GHZ State
qc.h(0)
qc.cx(0, 1)
qc.cx(0, 2)
qc.draw(output = 'mpl')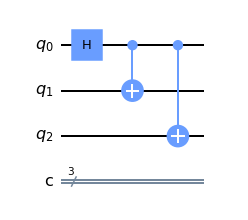
We can also create the same quantum state by calling the initialize() method on the Quantum Circuit and passing it the state vector for the state and the Qubits which have to be entangled.
# Creating Quantum Circuit
qc = QuantumCircuit(3, 3)
# Creating GHZ State
qc.initialize([1/np.sqrt(2), 0, 0, 0, 0, 0, 0, 1/np.sqrt(2)], qubits=[0, 1, 2])
qc.draw(output='mpl')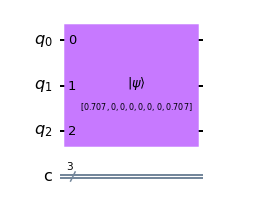
The Q-Sphere corresponding to the given state of Qubits is shown below, and confirms that the desired GHZ state has been achieved-