While Qubits can be in a state of superposition during computing, during measurement, any Qubit that is in a state of superposition will collapse onto one of the 2 basis pairs. Born Rule is used for predicting the probability with which a Qubit will collapse onto each of the basis pairs during measurement. While the most commonly used basis pairs are |0> and |1>, the rule can be used for any basis pairs.
Born Rule
Born Rule states that the probability of a state, say Ψ (psi) collapsing into a state |a>, p(a) when measuring onto basis pairs |a> and |a>† is given by-

Similarly, the probability of a state Ψ collapsing into state |a>†, p(a†) when measuring onto the same basis pairs |a> and |a>† is given by-
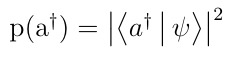
Alternatively, Since the state Ψ can only collapse into one of the basis pairs- |a> and |a>†, and the sum of probabilities of collapsing into both states is 1, the probability of a state Ψ collapsing into state |a>† can also be given by-
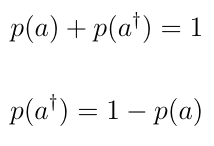
Example
In this example, we will calculate the probability of a state Ψ = 1/sqrt(2) |0> + 1/sqrt(2) |1> collapsing into states |0> and |1> on measurement.
Note– sqrt(2) represents square-root of 2.
Probability of Getting 0
The probability of Ψ collapsing into state |0> is given by-

After substituting the value of Ψ to 1/sqrt(2) |0> + 1/sqrt(2) |1>
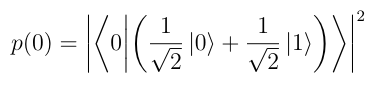
After simplifying, we get-

Substituting the value of <0|0> and <0|1> as 1 and 0 respectively, we get-

This gives the value of p(0), the probability of state Ψ collapsing into |0> as 0.5
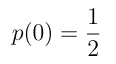
Probability of Getting 1
Similarly, we can calculate the probability of getting |1> on measuring the state Ψ
The probability of Ψ collapsing into state |1> is given by-
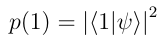
After substituting the value of Ψ to 1/sqrt(2) |0> + 1/sqrt(2) |1>
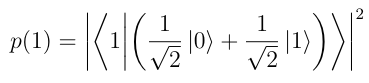
After simplifying, we get-
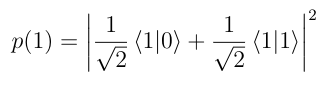
Substituting the value of <1|0> and <1|1> as 0 and 1 respectively, we get-

This gives the value of p(1), the probability of state Ψ collapsing into |1> as 0.5
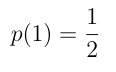
Notice that the sum of probabilities of the state Ψ collapsing into |0> and |1> during measurement is 1, as expected.
Also, notice that the probability of the state Ψ collapsing into the state is the square of its amplitude. The probability of state Ψ = 1/sqrt(2) |0> + 1/sqrt(2) |1>|0>1/sqrt(2)|1>1/sqrt(2).