Like Classical Computing, Quantum Computing also has gates. To differentiate them from their classical counterparts, we will frequently refer to them as Quantum Gates. Quantum Gates are used for manipulating the state of a Qubit. A Quantum Gate applied on a Qubit in a particular state can change the state of a Qubit. Although in some cases, a particular gate might not change the state of a Qubit in a particular state. In this chapter of the Qiskit Tutorial, you will get a brief overview of the various Single Qubit Quantum Gates. The following chapters will discuss some important Single Qubit Quantum Gates in detail. Several Quantum Gates also act on multiple Qubits, these will be covered in a later chapter.
Quantum Gates
Quantum Gates can be represented by a matrix. This matrix can be used to determine the effect of the Quantum Gate on a particular state. The new state of the Qubit can be known by multiplying the matrix for the Quantum Gate by the state of the Qubit.
Example†
In the following example, we calculate the new state of a Qubit after the application of X Gate on a Qubit in the state |0>. The new state ψ is calculated by multiplying the matrix for X Gate, represented by X with the state vector of the Qubit. The new state of the Qubit is |1>.
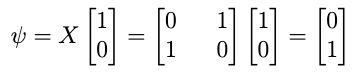
To summarize, the X Gate changed the state of the Qubit from |0> to |1>
Effect of Quantum Gates
Applying Quantum Gates on a Qubit can have an effect on the state of those Qubits. This change of state can be represented by the change in the state-vector of the Qubit or its representation on the Bloch Sphere.
Example†
In the following example, we consider the effect of the application of the X Gate on its Bloch Sphere Representation. The original state of the Qubit is |0>. After the application of X Gate, the state of the Qubit changes to |1>. This change can be seen in the state-vector representation of the Qubit. In the original state |0>, the state-vector pointed along the positive Z-axis. In the final state |1>, the state-vector pointed along the negative Z-axis.
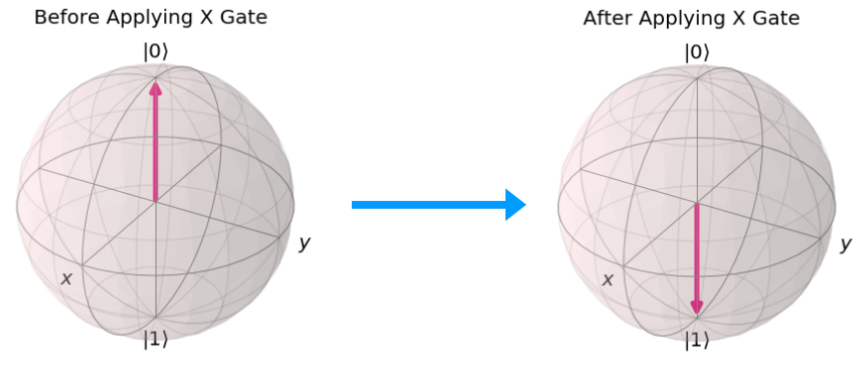
† It’s alright if you don’t know what is X Gate. You will get to know about the X Gate and various other gates in the following chapters. It is sufficient to know for now that applying Quantum Gates on Qubits can change the state of the Qubit.
Table of Single Qubit Quantum Gates
The following table covers various Single Qubit Quantum Gates in brief.
| Quantum Gate | Symbol | Effect on the Bloch Sphere | Comments |
|---|---|---|---|
| X | X | Rotates the State vector by π radians about the X-axis in anti-clockwise direction. | It is also known as NOT Gate and Bit flip gate because it reverses the probabilities of measuring 0 and 1 on measurement. Learn More |
| Y | Y | Rotates the State vector by π radians about the Y-axis in anti-clockwise direction. | It is also known as Bit and Phase flip gate because it performs both, phase flip like Z Gate and bit flip like X Gate. Learn More |
| Z | Z | Rotates the State vector by π radians about the Z-axis in anti-clockwise direction. | It is also known as Phase flip gate because it flips the phase of a Qubit. Learn More |
| Identity | I or Id | No effect on State vector. | It is useful when no operation is to be done on a Qubit. Learn More |
| Hadamard | H | Rotates the State vector by π radians about the XZ-axis in anti-clockwise direction. | It maps X-axis to Z-axis and vice versa. Learn More |
| RX | RX | Rotates the State vector by given radians about the X-axis in anti-clockwise direction. | It is a parameterized Gate. It performs rotations about X-axis by different amounts depending on the parameter. Learn More |
| RY | RY | Rotates the State vector by given radians about the Y-axis in anti-clockwise direction. | It is a parameterized Gate. It performs rotations about Y-axis by different amounts depending on the parameter. Learn More |
| RZ | RZ | Rotates the State vector by given radians about the Z-axis in anti-clockwise direction. * | It is a parameterized Gate. It performs rotations about Z-axis by different amounts depending on the parameter. Learn More |
| Phase | P | Rotates the State vector by given radians about the Z-axis in anti-clockwise direction. * | It is a parameterized Gate. It performs rotations about Z-axis by different amounts depending on the parameter. Learn More |
| S | S | Rotates the State vector by π/2 radians about the Z-axis in anti-clockwise direction. | It is also known as the Square-root of Z Gate. This is because applying S Gate twice has the same effect as a Z Gate. Learn More |
| S Dagger | Sdg or S† | Rotates the State vector by π/2 radians about the Z-axis in clockwise direction. | It is the inverse of S Gate. Learn More |
| T | T | Rotates the State vector by π/4 radians about the Z-axis in anti-clockwise direction. | It is also known as the fourth-root of Z Gate. This is because applying S Gate four times has the same effect as a Z Gate. Learn More |
| T Dagger | Tdg or T† | Rotates the State vector by π/4 radians about the Z-axis in clockwise direction. | It is the inverse of T Gate. Learn More |
| SX | SX | Rotates the State vector by π/2 radians about the X-axis in anti-clockwise direction. | It is also known as the Square-root of X Gate. This is because applying SX Gate twice has the same effect as an X Gate. Learn More |
| SX Dagger | SXdg or SX† | Rotates the State vector by π/2 radians about the X-axis in clockwise direction. | It is the inverse of SX Gate. Learn More |
* The RZ and Phase Gates have the same effect on a Qubit when applied with the same parameter. The difference between them is that their multi-Qubit versions have different effects. For example, a CP Gate will have a different effect as compared to a CRZ Gate. You will learn more about this in later chapters.