The Sdg Gate is a lesser used gate in Quantum Computing. Qiskit provides a method for applying Sdg Gate on a Qubit. In this chapter of the Qiskit Tutorial, you will learn about Sdg Gate and how to apply Sdg Gate on a Qubit in Qiskit.
Sdg Gate
The Sdg Gate acts on a single Qubit. The Sdg gate changes the phase of the Qubit by -90° or -π/2 radians. However, in terms of its effect on a state represented in terms of the standard basis pairs |0> and |1>, it has no effect on the coefficients of |0> to |1>. Hence, the application of Sdg Gate does not alter the probabilities of the state of the Qubit collapsing into |0> or |1> upon measurement.
Note– The Sdg Gate is a special case of Phase Gate where the parameter(the phase change) is -90° or -π/2 radians.
Note– The Sdg Gate is sometimes also called √Z Gate. This is because applying the Sdg Gate twice produces the same effect as a Z Gate.
Note– The Sdg Gate is also called S-dagger Gate or S† Gate(S with a Dagger in super-script).
Sdg Gate: Bloch Sphere
The Sdg Gate performs a rotation about the Z-axis on the Bloch Sphere by a 90° or π/2 radians in the clockwise direction.
Example
In this example, we will look at how the application of Sdg gate on the Qubit affects its representation on the Bloch Sphere. Remember how Sdg Gate performs a rotation by 90° or π/2 radians about the Z-axis on the Bloch Sphere in the clockwise direction.
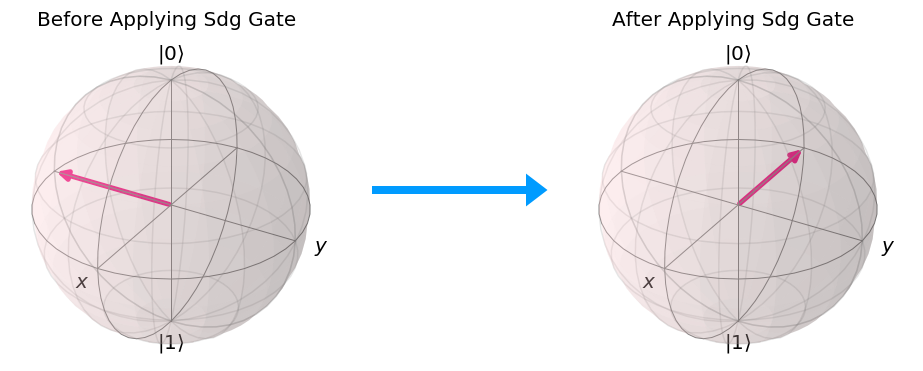
In the below figure, the Sdg Gate is applied on a Qubit in the state Ψ = |+> and the resulting state of the Qubit is Ψ = |-i>.
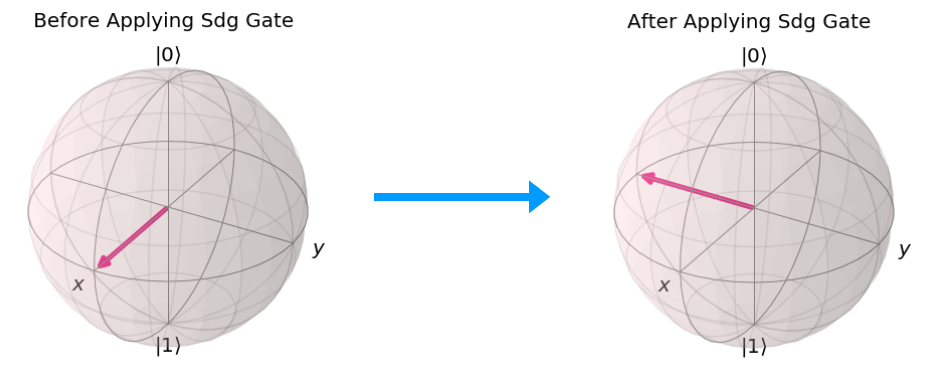
In the below figure, the Sdg Gate is applied on a Qubit in the state Ψ = |-i> and the resulting state of the Qubit is Ψ = |->.
Note– Since Sdg Gate actually performs rotation about the Z-axis, it will have no effect on a vector that lies on the Z-axis.
Sdg Gate: Matrix
The Sdg Gate in Quantum Computing is represented by the matrix Sdg
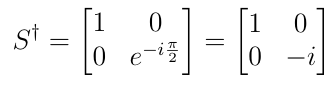
In the matrix, i represents square-root of -1.
The resulting state of a Qubit after the application of Sdg Gate can also be calculated by multiplying the Matrix for Sdg Gate with the vector representing the state of the Qubit.
Example
In this example, we will apply the Sdg gate to a Qubit, and calculate the resulting state by Multiplying it with the Matrix for Sdg Gate.
Let the state of the Qubit be Ψ = |+> = 1/sqrt(2)|0> + 1/sqrt(2) |1>
After Applying the Sdg Gate, the resulting state of the Qubit can be calculated by-
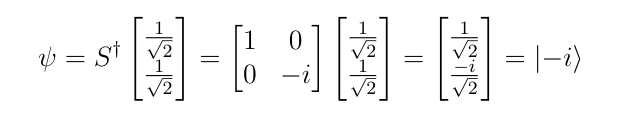
Since there is only rotation about the Z-axis, notice that the probability of getting |0> and |1> are the same whereas there is a change in the phase of the Qubit.
Inverse of Sdg Gate
The inverse of a Sdg Gate is S Gate. You have already learned about S Gate in the previous chapter. The Sdg Gate produces the effect of rotation by 90° or π/2 radians about the Z-axis on the Bloch Sphere in clockwise direction. The S Gate produces the effect of rotation by 90° or π/2 radians about the Z-axis on the Bloch Sphere in counter-clockwise direction. Since applying S Gate after applying S† Gate changes the state of the Qubit to the original state, S Gate is the inverse of S† Gate.
Sdg Gate in Qiskit
The Sdg Gate in Qiskit can be applied to any Qubit by calling the sdg() method on the Quantum Circuit(an instance of QuantumCircuit class) and passing it an integer for the Qubit on which Sdg Gate is to be applied.
Example
In this example, we will be applying Sdg Gate on the first Qubit in the Quantum Circuit, which will contain 2 Qubits.
# Creating a Quantum Register with 1 Qubit
qr = qiskit.QuantumRegister(2)
# Creating a Quantum Circuit
circuit = QuantumCircuit(qr)
# Applying Sdg Gate on the first Qubit
circuit.sdg(0)
# Drawing the Quantum Circuit
circuit.draw()This will result in the following Quantum Circuit being drawn-
Notice that the Sdg Gate is applied to the first Qubit. Also notice, that Qubits follow a 0 based indexing.