Qiskit: SXdg Gate

The SXdg Gate is a lesser used gate in Quantum Computing. Qiskit provides a method for applying SXdg Gate on a Qubit. In this chapter of the Qiskit Tutorial, you will learn about SXdg Gate and how to apply SXdg Gate on a Qubit in Qiskit.

SXdg Gate

The SXdg Gate acts on a single Qubit. The SXdg Gate performs the rotation about the X-axis of the Bloch Sphere by 90° or π/2 radians in the clockwise direction.

Note– The SXdg Gate is a special case of RX Gate where the parameter(the phase change) is -90° or -π/2 radians.

Note– The SXdg Gate is sometimes also called √X Gate. This is because applying the SXdg Gate twice produces the same effect as a X Gate.

SXdg Gate: Bloch Sphere

The SXdg Gate performs a rotation about the X-axis on the Bloch Sphere by a 90° or π/2 radians in the clockwise direction.

Example

In this example, we will look at how the application of SXdg gate on the Qubit affects its representation on the Bloch Sphere. Remember how SXdg Gate performs a rotation by 90° or π/2 radians about the X-axis on the Bloch Sphere in the clockwise direction.

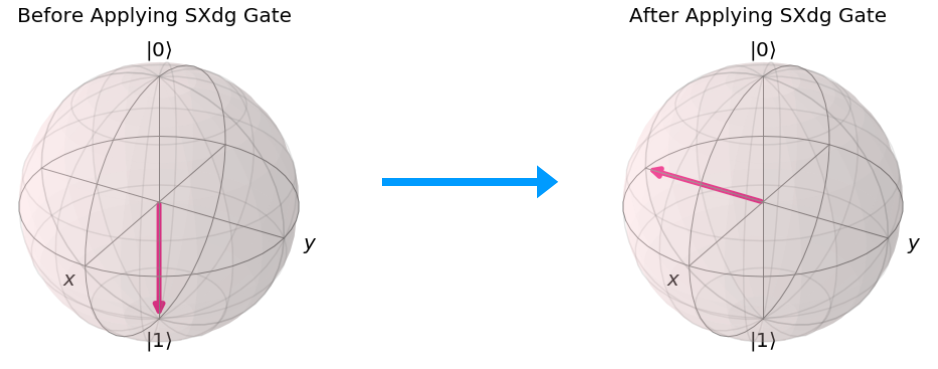
In the below figure, the SXdg Gate is applied on a Qubit in the state Ψ = |1> and the resulting state of the Qubit is Ψ = |-i>.

Effect of Applying SXdg Gate

In the below figure, the SXdg Gate is applied on a Qubit in the state Ψ = |i> and the resulting state of the Qubit is Ψ = |1>.

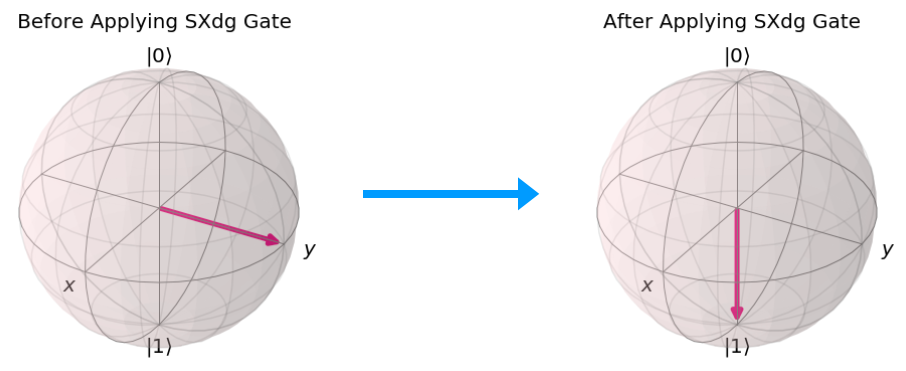
Effect of Applying SXdg Gate

Note– Since SXdg Gate actually performs rotation about the X-axis, it will have no effect on a vector that lies on the X-axis.

SXdg Gate: Matrix

The SXdg Gate in Quantum Computing is represented by the matrix SXdg

Matrix for SXdg Gate

In the matrix, i represents square-root of -1.

The resulting state of a Qubit after the application of SXdg Gate can also be calculated by multiplying the Matrix for SXdg Gate with the vector representing the state of the Qubit.

Example

In this example, we will apply the SXdg gate to a Qubit, and calculate the resulting state by Multiplying it with the Matrix for SXdg Gate.

Let the state of the Qubit be Ψ = |0>

After Applying the SXdg Gate, the resulting state of the Qubit can be calculated by-

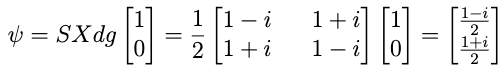
The resulting state is  Ψ = (1-i)/2 |0> + (1+i)/2 |1> , after removing the Global Phase, the state can be written as Ψ = 1/sqrt(2) |0> +i/sqrt(2) |1>, which is the same as that achieved by the desired rotation on the Bloch Sphere.

Inverse of SXdg Gate

The inverse of a SXdg Gate is SX Gate. The SXdg Gate produces the effect of rotation by 90° or π/2 radians about the X-axis on the Bloch Sphere in clockwise direction. The SX Gate produces the effect of rotation by 90° or π/2 radians about the X-axis on the Bloch Sphere in counter-clockwise direction. Since applying SX Gate after applying SXdg Gate changes the state of the Qubit to the original state, SX Gate is the inverse of SXdg Gate. You have learned about SX Gate in the previous chapter.

SXdg Gate in Qiskit

The SXdg Gate in Qiskit can be applied to any Qubit by calling the sxdg() method on the Quantum Circuit(an instance of QuantumCircuit class) and passing it an integer for the Qubit on which SXdg Gate is to be applied.

Example

In this example, we will be applying SXdg Gate on the first Qubit in the Quantum Circuit, which will contain 2 Qubits.

# Creating a Quantum Register with 2 Qubit
qr = qiskit.QuantumRegister(2)

# Creating a Quantum Circuit
circuit = QuantumCircuit(qr)

# Applying SXdg Gate on the first Qubit
circuit.sxdg(0)

# Drawing the Quantum Circuit
circuit.draw()

This will result in the following Quantum Circuit being drawn-

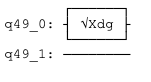
Applying Qiskit SXdg Gate

Notice that the SXdg Gate is applied to the first Qubit.