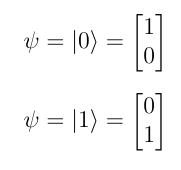In previous chapter of this Qiskit Tutorial, you studied that the probability of a state collapsing into 0 or 1 during measurement depends on the state of the Qubit at the time of measurement. The state of the Qubit is altered by performing operations on the Qubit such as applying various Quantum Gates. In this chapter of the Qiskit Tutorial, you will learn about representing a Quantum State such as state of a Qubit.
Representing a Quantum State
A Quantum State is denoted by ψ (psi). Any Quantum State, such as the state of a Qubit can be written in the form-
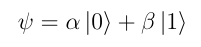
The coefficient of |0> (called ket 0), α is a complex number. Similarly, the coefficient of |1> (called ket 1), β is also a complex number. |0> and |1> are the basis pairs on which the state of the Qubit is measured. You will learn more about basis pairs in next chapter. For now, it is sufficient to know that any Quantum State can be measured using these basis pairs- just like every other basis pair, and there are infinite many of them. Additionally, |0> and |1> are the most common basis pairs for measuring the state of a Qubit. You will get to know the reason for this in the next section of this chapter.
Note– The state of any Qubit can be described by ψ = α|0> + β|1>. This includes the state of a Qubit in superposition.
Note– For the mathematically inclined, |0> and |1> (or any basis pairs) are orthonormal vectors.
Probabilities on Measurement
Since any Qubit in the state of superposition collapses into either 0 or 1 upon measurement with different probabilities depending on the state, the probabilities of measuring 0 and 1 can be obtained from the representation of the state.
The probability of measuring 0, p(0) and the the probability of measuring 1, p(1) for a Quantum State defined by ψ = α|0> + β|1> can be calculated as-
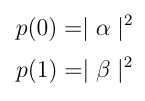
Measuring a Qubit can result in either measuring a 0 or a 1, therefore-
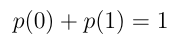
Note– α and β are also called amplitudes. The square of amplitude gives the measure of probability.
The state ψ = |0> will always result in 0 upon measurement, p(0) = 1. Similarly, the state ψ = |1> will always result in 1 upon measurement, p(1) = 1.
Example
In this example, we will calculate the probabilities of measuring 0 and 1 upon measurement of a Qubit in the state ψ = 1/sqrt(2) |0> + 1/sqrt(2) |1>
Note- sqrt(2) represents square-root of 2.
The probability of obtaining 0 on measurement can be calculated as-
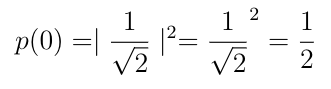
Similarly, the probability of obtaining 1 on measurement can be calculated as-
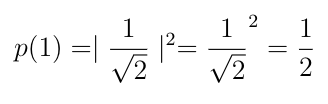
Since the coefficients of both |0> and |1> were equal, the probabilities of obtaining 0 and 1 on measurement are equal.
Also notice that the probabilities of measuring 0 and 1 add up to 1, as expected.
State as a Vector
The state of a Qubit can also be represented as a vector. For a Qubit that has state ψ = α|0> + β|1>,
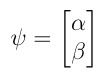
The state |0> and |1> can be represented as the following vectors-