In this blog post, we will be talking about how to use the algorithm of Nearest Neighbours for Classification with Scikit Learn. In an earlier post, we discussed about how to use the Nearest Neighbours algorithm to perform a regression task using Scikit-Learn. Further, we will be dealing only with binary classification in this post, i.e, the sample output will contain only 2 classes. There are no other pre-requisites to follow the blog other than having a basic knowledge Nearest Neighbour Algorithm works. This blog post is structured similar to the last blog post.
We start by making all the necessary imports. First we import the Scikit-Learn library and then we import the KNeighborsClassifier from sklearn.neighbors module. Then we create an object from this KNeighborsClassifier class, and let’s name it model.For now, we will set the value of n_neighbors to 1, i.e, the number of neighbours used to calculate the value of a new sample input.
import sklearn
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=1)
In this blog post too, we will not be working with any real dataset. We create some artificial data to train this model on. For now we are using only 4 samples of data for training, each with only 2 features and 1 target value. The X_train variable contains 8 samples, each of which contains 2 features. The y_train variable contains the the target values, 0 or 1, each of which denotes a separate class.
X_train=[[1, 1], [2, 2], [1, 2], [2, 1], [3, 1], [4, 1], [3, 2], [4, 2]]
y_train=[0, 0, 0, 0, 1, 1, 1, 1]
Now we train the model with this training data. We call the fit() method on the KNeighborsClassifier to train the model.
model.fit(X_train, y_train)
Next, we start making predictions for various values of input feature.
model.predict([[3.2, 1.2]])
We are making a prediction for the input features [3.2, 1.2]. Since, for now we are considering only 1 closest neighbour, the predicted class will be the same as that of the target value of its nearest neighbour. The nearest neighbour for the point [3.2, 1. 2] is [3, 1] and the class it belongs to is 1, hence the class of output for point [3.2, 1.2] will be 1 too.
>>>[1.]
Let’s make another prediction, this time for [1.1, 1.1].
model.predict([[1.1, 1.1]])
Again, the nearest neighbour to [1.1, 1.1] is [1, 1], and the class it belongs to is 0, hence the class of output for point [1.1, 1.1] will be 0 too.
>>>[0.]
Graphical Depiction
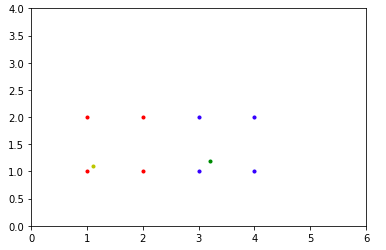
In the graph above, the red dots represent one class(class 0), while the blue dots represent another class(class 1). These are the data points or samples that were used to train the model. The data points in green and yellow represent the test instances 1 and 2 respectively. It can be clearly seen that the nearest neighbour of test instance 1(green dot) belongs to class 1(a blue dot). Similarly, the nearest neighbour of test-instance 2(yellow dot) belongs to class 0(a red dot).
Example 2
Now we will create a new model, like we did previously, but this time we will be set the value of n_neighbors to 3, so that the calculates the class of a new input by using the 3 nearest neighbours instead of just 1. The output will be computed by calculating which class has most number of samples within the first 3 nearest neighbours. So, for example, if the 3 nearest neighbours of a new test sample are 2 belonging to class 1 and 1 belonging to class 0, then the output class for a new test sample will be 1. This is because out of 3 nearest neighbours, a majority of them belong to class 1.
Next we train the model on the training data.
model = KNeighborsClassifier(n_neighbors=3)
model.fit(X_train, y_train)
Now we will use this model to predict the value of a new sample [2.7, 1]
model.predict([[2.7, 1]])
The 3 closest neighbours to [2.7, 1] are [3, 1], [2, 1] and [3, 2]. Out of these, [3, 1] and [3, 2] belong to class 1 and [2, 1] belongs to class 0. Hence, the output for this new test sample will be 1.
>>>[1.]
Graphical Depiction
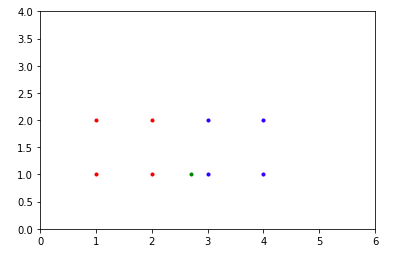
The graph above shows the training data, which is the same as in previous graph. Along with it, the new test sample(as a green dot) is also present in the graph. As it can be clearly seen from the graph, among the 3 nearest neighbours to the new test sample, 2 belong to class 1(blue dots) and one belongs to class 0(red dots).
Conclusion
In this blog post, we have discussed how to use the Algorithm of Nearest Neighbours for Classification with Scikit Learn. We have also taken 2 examples and demonstrated how the output values differ by using different values of nearest neighbours. In this post we have taken the example of Classification for the Nearest Neighbours. In future blog posts we will talk about the various modifications of the standard Nearest Neighbours Algorithms.
You can find the code for this blog on Github here.