Rectified Linear Unit, also known as ReLU overcame some of the serious disadvantages of the earlier used activation functions such as Sigmoid and Hyperbolic Tangent activation functions. These include the exploding gradients and vanishing gradients problem. ReLU overcame these problems and it was fast and simple to calculate. However, despite all this it was far from perfect. It came with its own set of disadvantages, such as being non-differentiable at 0. But the more serious one is that, during training times, it can cause something known as dead neurons. To overcome this serious defect of dying neurons, a new activation function was suggested, the Leaky ReLU activation function.
It is quite similar to the ReLU activation function, except that it just has a small leak. So instead of outputting a 0 for all negative values, it outputs a value of -αx when x is negative. For positive values of x, it simply outputs x. Mathematically, the Leaky ReLU activation function can be written as-
y = LeakyReLU(x) = max(αx, x)
The amount of leak is determined by the value of hyper-parameter α. It’s value is small and generally varies between 0.01 to 0.1-0.2. Similar to ReLU, Leaky ReLU is continuous everywhere but it is not differentiable at 0. The derivative of the function is 1 for x>0, and α for x<0.
The graph for Leaky ReLU function, with α=0.05 is shown below-
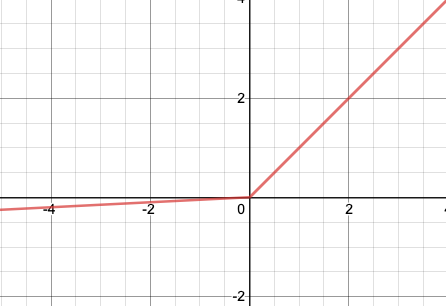
Due to this leak, the problem of dead neurons is avoided. Further, a research has found that Leaky ReLU activation functions outperformed the ReLU activation function. Further, Leaky ReLU activation functions with a higher value of leak perform better than those with lower value of leak.
Pros
- Performs better as compared to traditionally used activation functions such as Sigmoid and Hyperbolic-Tangent functions and even ReLU.
- It is fast and easy to calculate. The same applies to it’s derivative which is calculated during the backpropagation.
- It does not saturate for positive values of input and hence does not run into problems related to exploding/vanishing gradients during Gradient Descent.
- Does not suffer from dying ReLU problem.
Cons
- Though the function is continuous at all points, it is not differentiable at the point x=0, i.e, at the point x=0, the slope of the graph changes abruptly as can be seen in the graph. Due to this, during the gradient descent its value will ‘bounce around’. Despite this fact, Leaky ReLU works very well in practice.
- Unlike the Parameterised ReLU or PReLU, the value of α is defined prior to the training and hence cannot be adjusted during the training time. The value of α hence chosen might not be the most optimal value.